Easy Hyperparameter Tuning with Keras Tuner and TensorFlow

In this tutorial, you will learn how to use the Keras Tuner package for easy hyperparameter tuning with Keras and TensorFlow.

This tutorial is part four in our four-part series on hyperparameter tuning:

1. Introduction to hyperparameter tuning with scikit-learn and Python (first tutorial in this series)
2. Grid search hyperparameter tuning with scikit-learn ( GridSearchCV ) (tutorial from two weeks ago)
3. Hyperparameter tuning for Deep Learning with scikit-learn, Keras, and TensorFlow (last week’s post)
4. Easy Hyperparameter Tuning with Keras Tuner and TensorFlow (today’s post)

Last week we learned how to use scikit-learn to interface with Keras and TensorFlow to perform a randomized cross-validated hyperparameter search.

However, there are more advanced hyperparameter tuning algorithms, including Bayesian hyperparameter optimization and Hyperband, an adaptation and improvement to traditional randomized hyperparameter searches.

Both Bayesian optimization and Hyperband are implemented inside the keras tuner package. As we’ll see, utilizing Keras Tuner in your own deep learning scripts is as simple as a single import followed by single class instantiation — from there, it’s as simple as training your neural network just as you normally would!

Besides ease of use, you’ll find that Keras Tuner:

1. Integrates into your existing deep learning training pipeline with minimal code changes
2. Implements novel hyperparameter tuning algorithms
3. Can boost accuracy with minimal effort on your part

To learn how to tune hyperparameters with Keras Tuner, just keep reading.

Easy Hyperparameter Tuning with Keras Tuner and TensorFlow

In the first part of this tutorial, we’ll discuss the Keras Tuner package, including how it can help automatically tune your model’s hyperparameters with minimal code.

We’ll then configure our development environment and review our project directory structure.

We have several Python scripts to review today, including:

1. Our configuration file
2. The model architecture definition (which we’ll be tuning the hyperparameters to, including the number of filters in the CONV layer, learning rate, etc.)
3. Utilities to plot our training history
4. A driver script that glues all the pieces together and allows us to test various hyperparameter optimization algorithms, including Bayesian optimization, Hyperband, and traditional random search

We’ll wrap up this tutorial with a discussion of our results.

What is Keras Tuner, and how can it help us automatically tune hyperparameters?

Last week, you learned how to use scikit-learn’s hyperparameter searching functions to tune the hyperparameters of a basic feedforward neural network (including batch size, the number of epochs to train for, learning rate, and the number of nodes in a given layer).

While this method worked well (and gave us a nice boost in accuracy), the code wasn’t necessarily “pretty.”

And more importantly, it doesn’t make it easy for us to tune the “internal” parameters of a model architecture (e.g., the number of filters in a CONV layer, stride size, size of a POOL, dropout rate, etc.).

Libraries such as keras tuner make it dead simple to implement hyperparameter optimization into our training scripts in an organic manner:

• As we implement our model architecture, we define what ranges we want to search over for a given parameter (e.g., # of filters in our first CONV layer, # of filters in the second CONV layer, etc.)
• We then define an instance of either Hyperband, RandomSearch, or BayesianOptimization
• The keras tuner package takes care of the rest, running multiple trials until we converge on the best set of hyperparameters

It may sound complicated, but it’s quite easy once you dig into the code.

Additionally, if you are interested in learning more about the Hyperband algorithm, be sure to read Li et al.’s 2018 publication, Hyperband: A Novel Bandit-Based Approach to Hyperparameter Optimization.

To learn more about Bayesian hyperparameter optimization, refer to the slides from Roger Grosse, professor and researcher at the University of Toronto.

Configuring your development environment

To follow this guide, you need to have TensorFlow, OpenCV, scikit-learn, and Keras Tuner installed.

All of these packages are pip-installable:

$ pip install tensorflow # use "tensorflow-gpu" if you have a GPU
$ pip install opencv-contrib-python
$ pip install scikit-learn
$ pip install keras-tuner

Additionally, these two guides provide more details, help, and tips for installing Keras and TensorFlow on your machine:

• How to install TensorFlow 2.0 on Ubuntu
• How to install TensorFlow 2.0 on macOS

Either tutorial will help configure your system with all the necessary software for this blog post in a convenient Python virtual environment.

Having problems configuring your development environment?

All that said, are you:

• Short on time?
• Learning on your employer’s administratively locked system?
• Wanting to skip the hassle of fighting with the command line, package managers, and virtual environments?
• Ready to run the code right now on your Windows, macOS, or Linux systems?

Then join PyImageSearch University today!

Gain access to Jupyter Notebooks for this tutorial and other PyImageSearch guides that are pre-configured to run on Google Colab’s ecosystem right in your web browser! No installation required.

And best of all, these Jupyter Notebooks will run on Windows, macOS, and Linux!

Project structure

Before we can use Keras Tuner to tune the hyperparameters of our Keras/TensorFlow model, let’s first review our project directory structure.

Start by accessing the “Downloads” section of this tutorial to retrieve the source code.

From there, you’ll be presented with the following directory structure:

$ tree . --dirsfirst --filelimit 10
.
├── output
│   ├── bayesian [12 entries exceeds filelimit, not opening dir]
│   ├── hyperband [79 entries exceeds filelimit, not opening dir]
│   └── random [12 entries exceeds filelimit, not opening dir]
│   ├── bayesian_plot.png
│   ├── hyperband_plot.png
│   └── random_plot.png
├── pyimagesearch
│   ├── __init__.py
│   ├── config.py
│   ├── model.py
│   └── utils.py
└── train.py

2 directories, 8 files

Inside the pyimagesearch module, we have three Python scripts:

1. config.py: Contains important configuration options, such as the output path directory, input image dimensions, and number of unique class labels in our dataset
2. model.py: Contains the build_model function responsible for instantiating an instance of our model architecture; this function sets which hyperparameters will be tuned and the appropriate range of values for each hyperparameter
3. utils.py: Implements save_plot, a helper/convenience function to generate training history plots

The train.py script uses each of the implementations inside the pyimagesearch module to perform three types of hyperparameter searches:

1. Hyperband
2. Random
3. Bayesian optimization

The results of each of these experiments are saved to the output directory. The primary benefit of using a dedicated output directory for each experiment is that you can start, stop, and resume hyperparameter tuning experiments. This is especially important since hyperparameter tuning can take a considerable amount of time.

Creating our configuration file

Before we can use Keras Tuner to tune our hyperparameters, we first need to create a configuration file to store important variables.

Open the config.py file in your project directory structure and insert the following code:

# define the path to our output directory
OUTPUT_PATH = "output"

# initialize the input shape and number of classes
INPUT_SHAPE = (28, 28, 1)
NUM_CLASSES = 10

Line 2 defines our output directory path (i.e., where training history plots and hyperparameter tuning experiment logs are stored).

From there, we define the input spatial dimensions of the images in our dataset along with the total number of unique class labels (Lines 5 and 6).

Below we define our training variables:

# define the total number of epochs to train, batch size, and the
# early stopping patience
EPOCHS = 50
BS = 32
EARLY_STOPPING_PATIENCE = 5

For each experiment, we’ll allow our model to train for a maximum of 50 epochs. We’ll use a batch size of 32 for each experiment.

To short circuit experiments that do not show promising signs, we define an early stopping patience of 5, meaning if our accuracy does not improve after 5 epochs, we will kill the training process and move on to the next set of hyperparameters.

Tuning hyperparameters is a very computationally expensive process. If we can cut down on the number of trials that need to be run by killing off poorly performing experiments, we can save ourselves a tremendous amount of time.

Implementing our plotting helper function

After finding the optimal hyperparameters for our model, we’ll want to train the model on these hyperparameters and plot our training history (including loss and accuracy for both the training and validation sets).

To make the process easier, we can define a save_plot helper function inside the utils.py file.

Open this file now, and let’s take a look:

# set the matplotlib backend so figures can be saved in the background
import matplotlib
matplotlib.use("Agg")

# import the necessary package
import matplotlib.pyplot as plt

def save_plot(H, path):
	# plot the training loss and accuracy
	plt.style.use("ggplot")
	plt.figure()
	plt.plot(H.history["loss"], label="train_loss")
	plt.plot(H.history["val_loss"], label="val_loss")
	plt.plot(H.history["accuracy"], label="train_acc")
	plt.plot(H.history["val_accuracy"], label="val_acc")
	plt.title("Training Loss and Accuracy")
	plt.xlabel("Epoch #")
	plt.ylabel("Loss/Accuracy")
	plt.legend()
	plt.savefig(path)

The save_plot function requires us to pass in two variables: the training history H obtained from calling model.fit along with the path to the output plot.

We then plot the training loss, validation loss, training accuracy, and validation accuracy.

The resulting plot is saved to the output path.

Creating our CNN

Arguably the most important component of this tutorial is defining our CNN architecture, namely because this is where we set which hyperparameters we want to tune.

Open the model.py file inside the pyimagesearch module, and let’s see what’s going on:

# import the necessary packages
from . import config
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import BatchNormalization
from tensorflow.keras.layers import Conv2D
from tensorflow.keras.layers import MaxPooling2D
from tensorflow.keras.layers import Activation
from tensorflow.keras.layers import Flatten
from tensorflow.keras.layers import Dropout
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import Adam

Lines 2-11 import our required packages. Notice how we are importing the config file we created earlier in this guide.

The rest of these imports should look familiar to you if you have created CNNs with Keras and TensorFlow before. If not, I suggest you read my Keras tutorial, along with my book, Deep Learning for Computer Vision with Python.

Let’s now build our model:

def build_model(hp):
	# initialize the model along with the input shape and channel
	# dimension
	model = Sequential()
	inputShape = config.INPUT_SHAPE
	chanDim = -1

	# first CONV => RELU => POOL layer set
	model.add(Conv2D(
		hp.Int("conv_1", min_value=32, max_value=96, step=32),
		(3, 3), padding="same", input_shape=inputShape))
	model.add(Activation("relu"))
	model.add(BatchNormalization(axis=chanDim))
	model.add(MaxPooling2D(pool_size=(2, 2)))

The build_model function accepts a single object, hp, which is our hyperparameter tuning object from Keras Tuner. We’ll create the hp in our driver script, train.py, later in this tutorial.

Lines 16-18 initialize our model, grab the spatial dimensions of the input images in our dataset, and set the channel ordering (assuming “channels last”).

From there, Lines 21-26 define our first CONV => RELU => POOL layer set, the most important line being Line 22.

Here, we define our first hyperparameter to search over — the number of filters in our CONV layer.

Since the number of filters in a CONV layer is an integer, we use hp.Int to create an integer hyperparameter object.

The hyperparameter is given a name, conv_1, and can accept values in the range [32, 96] with steps of 32. This implies that valid values for conv_1 are 32, 64, 96.

Our hyperparameter tuner will automatically select the optimal value for this CONV layer that maximizes accuracy.

Similarly, we do the same thing for our second CONV => RELU => POOL layer set:

	# second CONV => RELU => POOL layer set
	model.add(Conv2D(
		hp.Int("conv_2", min_value=64, max_value=128, step=32),
		(3, 3), padding="same"))
	model.add(Activation("relu"))
	model.add(BatchNormalization(axis=chanDim))
	model.add(MaxPooling2D(pool_size=(2, 2)))

For our second CONV layer, we’re allowing more filters to be learned in the range [64, 128]. With a step size of 32, this implies that we’ll be testing values of 64, 96, 128.

We’ll do something similar for our number of fully connected nodes:

	# first (and only) set of FC => RELU layers
	model.add(Flatten())
	model.add(Dense(hp.Int("dense_units", min_value=256,
		max_value=768, step=256)))
	model.add(Activation("relu"))
	model.add(BatchNormalization())
	model.add(Dropout(0.5))

	# softmax classifier
	model.add(Dense(config.NUM_CLASSES))
	model.add(Activation("softmax"))

Lines 38 and 39 define our FC layer. We want to tune the number of nodes in this layer. We specify a minimum of 256 and a maximum of 768 nodes, allowing a step of 256.

Our next code block uses the hp.Choice function:

	# initialize the learning rate choices and optimizer
	lr = hp.Choice("learning_rate",
		values=[1e-1, 1e-2, 1e-3])
	opt = Adam(learning_rate=lr)

	# compile the model
	model.compile(optimizer=opt, loss="categorical_crossentropy",
		metrics=["accuracy"])

	# return the model
	return model

For our learning rate, we wish to see which of 1e-1, 1e-2, and 1e-3 performs best. Using hp.Choice will allow our hyperparameter tuner to select the best learning rate.

Finally, we compile the model and return it to the calling function.

Implementing hyperparameter tuning with Keras Tuner

Let’s put all the pieces together and learn how to tune Keras/TensorFlow hyperparameters using the Keras Tuner library.

Open the train.py file in your project directory structure, and let’s get started:

# import the necessary packages
from pyimagesearch import config
from pyimagesearch.model import build_model
from pyimagesearch import utils
from tensorflow.keras.callbacks import EarlyStopping
from tensorflow.keras.datasets import fashion_mnist
from tensorflow.keras.utils import to_categorical
from tensorflow.keras import backend as K
from sklearn.metrics import classification_report
import kerastuner as kt
import numpy as np
import argparse
import cv2

Lines 2-13 import our required Python packages. Notable imports include:

• config: Our configuration file
• build_model: Accepts a hyperparameter tuning object which selects various values to test for CONV filters, FC nodes, and learning rate — the resulting model is constructed and returned to the calling function
• utils: Used for plotting our training history
• EarlyStopping: A Keras/TensorFlow callback used to short circuit hyperparameter tuning experiments that are performing poorly
• fashion_mnist: The Fashion MNIST dataset that we’ll be training our model on
• kerastuner: The Keras Tuner package used to implement hyperparameter tuning

Next comes our command line arguments:

# construct the argument parser and parse the arguments
ap = argparse.ArgumentParser()
ap.add_argument("-t", "--tuner", required=True, type=str,
	choices=["hyperband", "random", "bayesian"],
	help="type of hyperparameter tuner we'll be using")
ap.add_argument("-p", "--plot", required=True,
	help="path to output accuracy/loss plot")
args = vars(ap.parse_args())

We have two command line arguments to parse:

1. The type of hyperparameter optimizer we’ll be using
2. The path to the output training history plot

From there, load the Fashion MNIST dataset from disk:

# load the Fashion MNIST dataset
print("[INFO] loading Fashion MNIST...")
((trainX, trainY), (testX, testY)) = fashion_mnist.load_data()

# add a channel dimension to the dataset
trainX = trainX.reshape((trainX.shape[0], 28, 28, 1))
testX = testX.reshape((testX.shape[0], 28, 28, 1))

# scale data to the range of [0, 1]
trainX = trainX.astype("float32") / 255.0
testX = testX.astype("float32") / 255.0

# one-hot encode the training and testing labels
trainY = to_categorical(trainY, 10)
testY = to_categorical(testY, 10)

# initialize the label names
labelNames = ["top", "trouser", "pullover", "dress", "coat",
	"sandal", "shirt", "sneaker", "bag", "ankle boot"]

Line 26 loads Fashion MNIST, pre-split into training and testing sets.

We then add a channel dimension to the dataset (Lines 29 and 30), scale the pixel intensities from the range [0, 255] to [0, 1] (Lines 33 and 34), and then one-hot encode the labels (Lines 37 and 38).

As mentioned during the imports section of this script, we’ll be using EarlyStopping to short circuit hyperparameter trials that are not performing well:

# initialize an early stopping callback to prevent the model from
# overfitting/spending too much time training with minimal gains
es = EarlyStopping(
	monitor="val_loss",
	patience=config.EARLY_STOPPING_PATIENCE,
	restore_best_weights=True)

We’ll monitor validation loss. If validation loss fails to improve significantly after EARLY_STOPPING_PATIENCE total epochs, then we’ll kill the trial and move on to the next one.

Keep in mind that tuning hyperparameters is an extremely computationally expensive process, so if we can kill off poorly performing trials, we can save ourselves a bunch of time.

The next step is to initialize our hyperparameter optimizer:

# check if we will be using the hyperband tuner
if args["tuner"] == "hyperband":
	# instantiate the hyperband tuner object
	print("[INFO] instantiating a hyperband tuner object...")
	tuner = kt.Hyperband(
		build_model,
		objective="val_accuracy",
		max_epochs=config.EPOCHS,
		factor=3,
		seed=42,
		directory=config.OUTPUT_PATH,
		project_name=args["tuner"])

Lines 52-62 handle if we wish to use the Hyperband tuner. The Hyperband tuner is a combination of random search with “adaptive resource allocation and early stopping.” It is essentially an implementation of Li et al.’s paper, Hyperband: A Novel Bandit-Based Approach to Hyperparameter Optimization.

If we supply a value of random as our --tuner command line argument then we’ll use a basic random hyperparameter search:

# check if we will be using the random search tuner
elif args["tuner"] == "random":
	# instantiate the random search tuner object
	print("[INFO] instantiating a random search tuner object...")
	tuner = kt.RandomSearch(
		build_model,
		objective="val_accuracy",
		max_trials=10,
		seed=42,
		directory=config.OUTPUT_PATH,
		project_name=args["tuner"])

Otherwise, we’ll assume we are using Bayesian optimization:

# otherwise, we will be using the bayesian optimization tuner
else:
	# instantiate the bayesian optimization tuner object
	print("[INFO] instantiating a bayesian optimization tuner object...")
	tuner = kt.BayesianOptimization(
		build_model,
		objective="val_accuracy",
		max_trials=10,
		seed=42,
		directory=config.OUTPUT_PATH,
		project_name=args["tuner"])

Once our hyperparameter tuner is instantiated we can search the space:

# perform the hyperparameter search
print("[INFO] performing hyperparameter search...")
tuner.search(
	x=trainX, y=trainY,
	validation_data=(testX, testY),
	batch_size=config.BS,
	callbacks=[es],
	epochs=config.EPOCHS
)

# grab the best hyperparameters
bestHP = tuner.get_best_hyperparameters(num_trials=1)[0]
print("[INFO] optimal number of filters in conv_1 layer: {}".format(
	bestHP.get("conv_1")))
print("[INFO] optimal number of filters in conv_2 layer: {}".format(
	bestHP.get("conv_2")))
print("[INFO] optimal number of units in dense layer: {}".format(
	bestHP.get("dense_units")))
print("[INFO] optimal learning rate: {:.4f}".format(
	bestHP.get("learning_rate")))

Lines 90-96 kick off the hyperparameter tuning process.

After the tuning process is complete, we obtain the best hyperparameters (Line 99) and display on our terminal the optimal:

• Number of filters in the first CONV layer
• Number of filters in the second CONV layer
• Number of nodes in the fully connected layer
• Optimal learning rate

Once we have the best hyperparameters we need to instantiate a new model based on them:

# build the best model and train it
print("[INFO] training the best model...")
model = tuner.hypermodel.build(bestHP)
H = model.fit(x=trainX, y=trainY,
	validation_data=(testX, testY), batch_size=config.BS,
	epochs=config.EPOCHS, callbacks=[es], verbose=1)

# evaluate the network
print("[INFO] evaluating network...")
predictions = model.predict(x=testX, batch_size=32)
print(classification_report(testY.argmax(axis=1),
	predictions.argmax(axis=1), target_names=labelNames))

# generate the training loss/accuracy plot
utils.save_plot(H, args["plot"])

Line 111 takes care of building a model with our best hyperparameters.

A call to model.fit on Lines 112-114 trains our model on the best hyperparameters.

After training is complete, we perform a full evaluation of our testing set (Lines 118-120).

Finally, the resulting training history plot is saved to disk using our save_plot utility function.

Hyperparameter tuning with Hyperband

Let’s see the results of applying the Hyperband optimizer with Keras Tuner.

Start by accessing the “Downloads” section of this tutorial to retrieve the source code.

From there, open a terminal and execute the following command:

$ time python train.py --tuner hyperband --plot output/hyperband_plot.png
[INFO] loading Fashion MNIST...
[INFO] instantiating a hyperband tuner object..."
[INFO] performing hyperparameter search...

Search: Running Trial #1

Hyperparameter    |Value             |Best Value So Far
conv_1            |96                |?
conv_2            |96                |?
dense_units       |512               |?
learning_rate     |0.1               |?

Epoch 1/2
1875/1875 [==============================] - 119s 63ms/step - loss: 3.2580 - accuracy: 0.6568 - val_loss: 3.9679 - val_accuracy: 0.7852
Epoch 2/2
1875/1875 [==============================] - 79s 42ms/step - loss: 3.5280 - accuracy: 0.7710 - val_loss: 2.5392 - val_accuracy: 0.8167

Trial 1 Complete [00h 03m 18s]
val_accuracy: 0.8166999816894531

Best val_accuracy So Far: 0.8285999894142151
Total elapsed time: 00h 03m 18s

The Keras Tuner package works by running several “trials.” Here, we can see that during the first trial, we’ll experiment with 96 filters for the first CONV layer, 96 filters for the second CONV layer, a total of 512 nodes for our fully connected layer, and a learning rate of 0.1.

As our trials finish, the Best Value So Far column will be updated to reflect the best hyperparameters found.

Notice, though, that we only train this model for a total of two epochs — this is due to our EarlyStopping stopping criterion. If our validation accuracy doesn’t improve by a certain amount, we’ll short circuit the training process to avoid spending too much time exploring hyperparameters that won’t increase our accuracy significantly.

Thus, at the end of the first trial, we’re sitting at 82% accuracy.

Let’s now jump to the final trial:

Search: Running Trial #76

Hyperparameter    |Value             |Best Value So Far   
conv_1            |32                |64
conv_2            |64                |128
dense_units       |768               |512
learning_rate     |0.01              |0.001

Epoch 1/17
1875/1875 [==============================] - 41s 22ms/step - loss: 0.8586 - accuracy: 0.7624 - val_loss: 0.4307 - val_accuracy: 0.8587
...
Epoch 17/17
1875/1875 [==============================] - 40s 21ms/step - loss: 0.2248 - accuracy: 0.9220 - val_loss: 0.3391 - val_accuracy: 0.9089

Trial 76 Complete [00h 11m 29s]
val_accuracy: 0.9146000146865845

Best val_accuracy So Far: 0.9289000034332275
Total elapsed time: 06h 34m 56s

The best validation accuracy found thus far is 92%.

After Hyperband finishes running, we see the optimal parameters displayed on our terminal:

[INFO] optimal number of filters in conv_1 layer: 64
[INFO] optimal number of filters in conv_2 layer: 128
[INFO] optimal number of units in dense layer: 512
[INFO] optimal learning rate: 0.0010

For our first CONV layer, we see that 64 filters are best. The next CONV layer in the network likes 128 layers — this isn’t an entirely surprising finding. Typically as we go deeper into a CNN, and as the spatial dimensions of the volume size decrease, the number of filters increases.

AlexNet, VGGNet, ResNet, and nearly all other popular CNN architectures have this type of pattern.

The final FC layer has 512 nodes, while our optimal learning rate is 1e-3.

Let’s train a CNN with these hyperparameters now:

[INFO] training the best model...
Epoch 1/50
1875/1875 [==============================] - 69s 36ms/step - loss: 0.5655 - accuracy: 0.8089 - val_loss: 0.3147 - val_accuracy: 0.8873
...
Epoch 11/50
1875/1875 [==============================] - 67s 36ms/step - loss: 0.1163 - accuracy: 0.9578 - val_loss: 0.3201 - val_accuracy: 0.9088
[INFO] evaluating network...
              precision    recall  f1-score   support

         top       0.83      0.92      0.87      1000
     trouser       0.99      0.99      0.99      1000
    pullover       0.83      0.92      0.87      1000
       dress       0.93      0.93      0.93      1000
        coat       0.90      0.83      0.87      1000
      sandal       0.99      0.98      0.99      1000
       shirt       0.82      0.70      0.76      1000
     sneaker       0.94      0.99      0.96      1000
         bag       0.99      0.98      0.99      1000
  ankle boot       0.99      0.95      0.97      1000

    accuracy                           0.92     10000
   macro avg       0.92      0.92      0.92     10000
weighted avg       0.92      0.92      0.92     10000


real    407m28.169s
user    2617m43.104s
sys     51m46.604s

After training for 50 epochs on our best hyperparameters, we obtain 92% accuracy on our validation set.

The total hyperparameter search and training time on my 3 GHz Intel Xeon W processor is 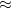6.7 hours. Using a GPU would reduce the training time considerably.

Hyperparameter tuning with random search

Let’s now look at a vanilla random search.

Again, be sure to access the “Downloads” section of this tutorial to retrieve the source code and example images.

From there, you can execute the following command:

$ time python train.py --tuner random --plot output/random_plot.png
[INFO] loading Fashion MNIST...
[INFO] instantiating a random search tuner object...
[INFO] performing hyperparameter search...

Search: Running Trial #1

Hyperparameter    |Value             |Best Value So Far
conv_1            |64                |?
conv_2            |64                |?
dense_units       |512               |?
learning_rate     |0.01              |?

Epoch 1/50
1875/1875 [==============================] - 51s 27ms/step - loss: 0.7210 - accuracy: 0.7758 - val_loss: 0.4748 - val_accuracy: 0.8668
...
Epoch 14/50
1875/1875 [==============================] - 49s 26ms/step - loss: 0.2180 - accuracy: 0.9254 - val_loss: 0.3021 - val_accuracy: 0.9037

Trial 1 Complete [00h 12m 08s]
val_accuracy: 0.9139999747276306

Best val_accuracy So Far: 0.9139999747276306
Total elapsed time: 00h 12m 08s

At the end of our first trial, we are obtaining 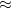91% accuracy on our validation set with 64 filters for the first CONV layer, 64 filters for the second CONV layer, a total of 512 nodes in the FC layer, and a learning rate of 1e-2.

By the 10th trial, our accuracy has improved, but not as big of a jump as it was with Hyperband:

Search: Running Trial #10

Hyperparameter    |Value             |Best Value So Far   
conv_1            |96                |96
conv_2            |64                |64
dense_units       |512               |512
learning_rate     |0.1               |0.001

Epoch 1/50
1875/1875 [==============================] - 64s 34ms/step - loss: 3.8573 - accuracy: 0.6515 - val_loss: 1.3178 - val_accuracy: 0.7907
...
Epoch 6/50
1875/1875 [==============================] - 63s 34ms/step - loss: 4.2424 - accuracy: 0.8176 - val_loss: 622.4448 - val_accuracy: 0.8295

Trial 10 Complete [00h 06m 20s]
val_accuracy: 0.8640999794006348
Total elapsed time: 01h 47m 02s

Best val_accuracy So Far: 0.9240000247955322
Total elapsed time: 01h 47m 02s

We’re now up to 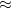92% accuracy. Still, the good news is that we’ve only spent 1h47m exploring the hyperparameter space (as opposed to 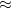6h30m from the Hyperband trials).

Below we can see the optimal hyperparameters that the randomized search found:

[INFO] optimal number of filters in conv_1 layer: 96
[INFO] optimal number of filters in conv_2 layer: 64
[INFO] optimal number of units in dense layer: 512
[INFO] optimal learning rate: 0.0010

The output of our randomized search is a bit different from that of Hyperband tuning. The first CONV layer has 96 filters while the second has 64 (Hyperband had 64 and 128, respectively).

That said, both randomized search and Hyperband agreed on 512 nodes in the FC layer and a learning rate of 1e-3.

After training we reach approximately the same validation accuracy as Hyperband:

[INFO] training the best model...
Epoch 1/50
1875/1875 [==============================] - 64s 34ms/step - loss: 0.5682 - accuracy: 0.8157 - val_loss: 0.3227 - val_accuracy: 0.8861
...
Epoch 13/50
1875/1875 [==============================] - 63s 34ms/step - loss: 0.1066 - accuracy: 0.9611 - val_loss: 0.2636 - val_accuracy: 0.9251
[INFO] evaluating network...
              precision    recall  f1-score   support

         top       0.85      0.91      0.88      1000
     trouser       0.99      0.98      0.99      1000
    pullover       0.88      0.89      0.88      1000
       dress       0.94      0.90      0.92      1000
        coat       0.82      0.93      0.87      1000
      sandal       0.97      0.99      0.98      1000
       shirt       0.82      0.69      0.75      1000
     sneaker       0.96      0.95      0.96      1000
         bag       0.99      0.99      0.99      1000
  ankle boot       0.97      0.96      0.97      1000

    accuracy                           0.92     10000
   macro avg       0.92      0.92      0.92     10000
weighted avg       0.92      0.92      0.92     10000


real    120m52.354s
user    771m17.324s
sys     15m10.248s

While 92% accuracy is essentially identical to that of Hyperband, a random search cuts our hyperparameter search time by 3x, which is a huge improvement by itself.

Hyperparameter tuning with Bayesian optimization

Let’s see how Bayesian optimization performance compares to Hyperband and randomized search.

Be sure to access the “Downloads” section of this tutorial to retrieve the source code.

From there, let’s give the Bayesian hyperparameter optimization a try:

$ time python train.py --tuner bayesian --plot output/bayesian_plot.png
[INFO] loading Fashion MNIST...
[INFO] instantiating a bayesian optimization tuner object...
[INFO] performing hyperparameter search...

Search: Running Trial #1

Hyperparameter    |Value             |Best Value So Far
conv_1            |64                |?
conv_2            |64                |?
dense_units       |512               |?
learning_rate     |0.01              |?

Epoch 1/50
1875/1875 [==============================] - 143s 76ms/step - loss: 0.7434 - accuracy: 0.7723 - val_loss: 0.5290 - val_accuracy: 0.8095
...
Epoch 12/50
1875/1875 [==============================] - 50s 27ms/step - loss: 0.2210 - accuracy: 0.9223 - val_loss: 0.4138 - val_accuracy: 0.8693

Trial 1 Complete [00h 11m 45s]
val_accuracy: 0.9136999845504761

Best val_accuracy So Far: 0.9136999845504761
Total elapsed time: 00h 11m 45s

During our first trial, we hit 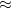91% accuracy.

By the final trial, we’ve boosted our accuracy slightly:

Search: Running Trial #10

Hyperparameter    |Value             |Best Value So Far   
conv_1            |64                |32
conv_2            |96                |96
dense_units       |768               |768
learning_rate     |0.001             |0.001

Epoch 1/50
1875/1875 [==============================] - 64s 34ms/step - loss: 0.5743 - accuracy: 0.8140 - val_loss: 0.3341 - val_accuracy: 0.8791
...
Epoch 16/50
1875/1875 [==============================] - 62s 33ms/step - loss: 0.0757 - accuracy: 0.9721 - val_loss: 0.3104 - val_accuracy: 0.9211

Trial 10 Complete [00h 16m 41s]
val_accuracy: 0.9251999855041504

Best val_accuracy So Far: 0.9283000230789185
Total elapsed time: 01h 47m 01s

We’re now obtaining 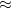92% accuracy.

The optimal hyperparameters found by Bayesian optimization are listed below:

[INFO] optimal number of filters in conv_1 layer: 32
[INFO] optimal number of filters in conv_2 layer: 96
[INFO] optimal number of units in dense layer: 768
[INFO] optimal learning rate: 0.0010

The following list breaks down the hyperparameters:

• Our first CONV layer has 32 nodes (versus 64 for Hyperband and 96 for random)
• The second CONV layer has 96 nodes (Hyperband selected 128 and random search 64)
• The fully connected layer has 768 nodes (both Hyperband and random search selected 512)
• Our learning rate is 1e-3 (all three hyperparameter optimizers agreed here)

Let’s now train our network on these hyperparameters:

[INFO] training the best model...
Epoch 1/50
1875/1875 [==============================] - 49s 26ms/step - loss: 0.5764 - accuracy: 0.8164 - val_loss: 0.3823 - val_accuracy: 0.8779
...
Epoch 14/50
1875/1875 [==============================] - 47s 25ms/step - loss: 0.0915 - accuracy: 0.9665 - val_loss: 0.2669 - val_accuracy: 0.9214
[INFO] evaluating network...
              precision    recall  f1-score   support

         top       0.82      0.93      0.87      1000
     trouser       1.00      0.99      0.99      1000
    pullover       0.86      0.92      0.89      1000
       dress       0.93      0.91      0.92      1000
        coat       0.90      0.86      0.88      1000
      sandal       0.99      0.99      0.99      1000
       shirt       0.81      0.72      0.77      1000
     sneaker       0.96      0.98      0.97      1000
         bag       0.99      0.98      0.99      1000
  ankle boot       0.98      0.96      0.97      1000

    accuracy                           0.92     10000
   macro avg       0.93      0.92      0.92     10000
weighted avg       0.93      0.92      0.92     10000


real    118m11.916s
user    740m56.388s
sys     18m2.676s

Accuracy has improved a bit here. We’re now at 93% accuracy using Bayesian optimization (both Hyperband and random search reported 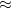92% accuracy).

How do we interpret these results?

Let’s now take a second to discuss these results. Since Bayesian optimization returned the highest accuracy, does that mean you should always use Bayesian hyperparameter optimization?

No, not necessarily.

Instead, I suggest running a few trials with each hyperparameter optimizer so you can get an idea of the “agreement level” of hyperparameters across several algorithms. If all three hyperparameter tuners are reporting similar hyperparameters, then you can be reasonably confident that you found the optimal ones.

Speaking of which, the following table breaks down the hyperparameter results for each optimizer:

While there was some disagreement on the number of CONV filters and the number of FC nodes, all three agreed that 1e-3 is the optimal learning rate.

What does that tell us?

Well, given that there was variation in the other hyperparameters, but the learning rate was the same across all three optimizers, we can conclude that the learning rate has the biggest impact on accuracy. The other parameters are less important than simply getting the learning rate right.

Summary

In this tutorial, you learned how to easily tune your neural network hyperparameters using Keras Tuner and TensorFlow.

The Keras Tuner package makes it dead simple to tune your model hyperparameters by:

• Requiring just a single import
• Allowing you to define the values and ranges inside your model architecture
• Interfacing directly with Keras and TensorFlow
• Implementing state-of-the-art hyperparameter optimizers

When training your own neural networks, I suggest you spend at least some time tuning your hyperparameters as you’ll likely be able to get anywhere from a 1-2% bump in accuracy (lower end) up to a 25% boost (higher end). Still, again, that is dependent on the specifics of your project.

To download the source code to this post (and be notified when future tutorials are published here on PyImageSearch), simply enter your email address in the form below!

The post Easy Hyperparameter Tuning with Keras Tuner and TensorFlow appeared first on PyImageSearch.